The basic idea to calculating the probabilities is to find the size of the area of the square where the center of the die can rest without touching/overlapping one of the edges.
In the case where the sides of the die are parallel to the sides of the square, this value is easy to compute. Where S is the side-length of the square, and D is the side-length of the die, then the acceptable area is 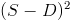 , giving us a probability of
, giving us a probability of 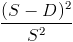 . Using real-world values of S = 2" and D = 5/8", we get a probability of 47% that the die will land entirely within the bounds of the square.
. Using real-world values of S = 2" and D = 5/8", we get a probability of 47% that the die will land entirely within the bounds of the square.
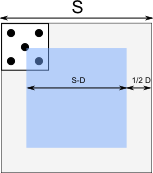
Matters get more complicated when the die lands at an angle. The center of the die must now remain a greater distance from the edge of the square - the horizontal distance from the center of the die to the left-most corner, for example. Because of symmetry, we know that this distance is half of the horizontal distance between the left-most and right-most corners, so let's compute that.
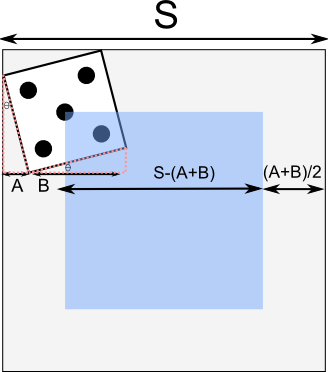
The angle between the side of the die and the square we will call θ. The distance A is simply D sin(θ), while the distance B is D cos(θ). This gives us a revised probability of 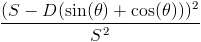 . At θ = 0, this gives us our old formula of
. At θ = 0, this gives us our old formula of 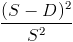 , while at θ = 45°, we get
, while at θ = 45°, we get 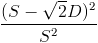 , which is the expected value.
, which is the expected value.
This formula only takes into account a single angle. To take into consideration all possible such angles, we must integrate it. Because of rotational and reflectional symmetry, we need only concern ourselves with rotations up to 45°, as after that point, it will start repeating a previous configuraiton. The integral is 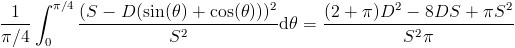 .
.
To reflect the fact that it can be difficult to determine whether or not a roll counts as over the edge, we can take into account a margin around the square. The die can land on or over the edge, and still count in the square, so long as none of its corners exceed the bounds of the margin. If the width of the margin is M, then this has the effect of increasing the side-length of the square by 2M, but only for deciding whether or not the die landed out of bounds. Our new formula is therefore 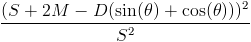 .
.
Integrating, we get 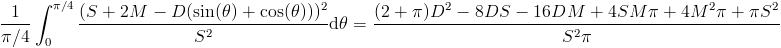 .
.
A calculator:
Square side length:
Die side length:
Margin:
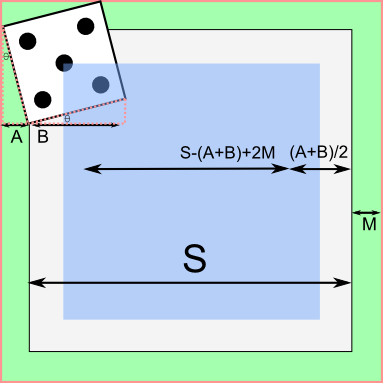
Things get much trickier when we want to ensure that at least two corners are outside of the square. For this, we'll ignore the margin. In the case that the die's sides are parallel, this is identical to the case above; if one of the corners is outside, at least one other must be as well. Compare with the 45° rotated die, on the other hand, where the only time you'll have two corners of the die out is when the die is resting in one of the corners of the square! Our approach must be able to handle both cases.
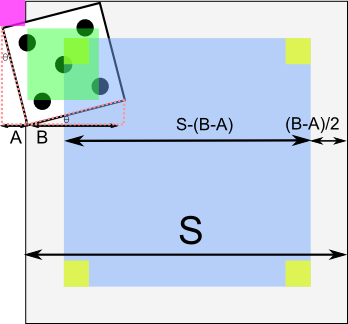
First, let's examine the cases where one of the corners it outside of the square. Assume without loss of generality that the die is resting on the left edge of the square, with the top-left corner resting in the adjacent square. There is a range of (translational) motion available to the die where the top-left die remains outside, while the bottom-left remains inside. This distance, labeled A in the diagram below, is equal to D sin(θ). Since this value is added to the margin on both sides, we get a partial formula of 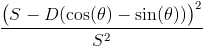 . In essence, we are dealing with a virtually smaller die (indicated in green in the diagram below).
. In essence, we are dealing with a virtually smaller die (indicated in green in the diagram below).
The above calculation, however, doesn't take into account the cases where corners are crossing two separate edges. This occurs when the center of the die is in one of the four squares marked in yellow in the diagram below. The side-length of each of these squares is equal to the distance the die can travel towards one of the edges, between the point where the first corner crosses and the second crosses. In other words, it's the value A that we calculated earlier. This can be observed by looking at the purple square, which is the same size as the yellow ones. When we subtract these four squares from the 'safe' area, we get 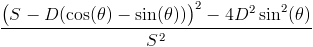 . Notice that when θ = 0, we get our original formula for a parallel die, while when θ = 45°, the cos(θ) and sin(θ) cancel out, leaving only the four squares.
. Notice that when θ = 0, we get our original formula for a parallel die, while when θ = 45°, the cos(θ) and sin(θ) cancel out, leaving only the four squares.
Integrating this formula, we get 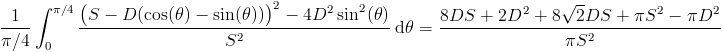 .
.
A calculator:
Square side length:
Die side length: